基本概念
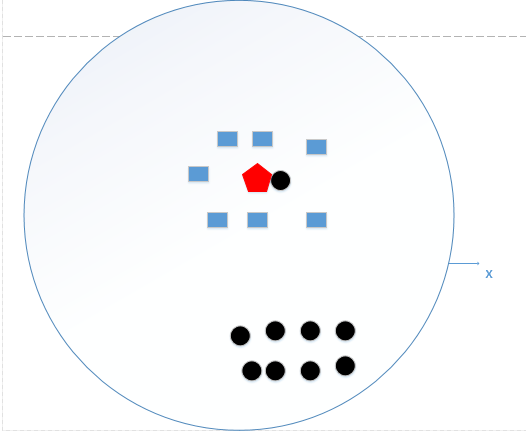
K近邻算法,即是给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。如下图:

如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。这也就是我们的目的,来了一个新的数据点,我要得到它的类别是什么?好的,下面我们根据k近邻的思想来给绿色圆点进行分类。
- 如果K=3,绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形,**少数从属于多数,**基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
- 如果K=5,绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形,**还是少数从属于多数,**基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
从上面例子我们可以看出,k近邻的算法思想非常的简单,也非常的容易理解,那么我们是不是就到此结束了,该算法的原理我们也已经懂了,也知道怎么给新来的点如何进行归类,只要找到离它最近的k个实例,哪个类别最多即可。
距离的度量
距离的度量一般使用欧式距离,L_p距离或者 Minkowsji距离:

K值的选择
如果K值选择比较小,相对而言误差也就会比较少,但是容易发生过拟合的现象.假设K=1,则样本中的噪声会对模型产生比较大的影响.
如果K值选择过大就会产生比较大的误差,造成误判的现象比较严重.假设K=N,就会输出所有样本中占比比较大的类型,而忽略掉其他类型.
所以我们需要的K值不能太大也不能太小.
在实际应用中K值一般取比较小的值,通常采用交叉验证的方法选取最优的K值.
优缺点
优点:简单、易于理解、容易实现、通过对K的选择可具备丢噪音数据的健壮性.
缺点:需要大量的空间储存已知的实例、算法的复杂度高.因为这类样本实例的数量过大,但这个新的未知实例实际并未接近目标样本.