Dropout出现的原因
具有大量参数的深度神经网络是非常强大的机器学习算法。但是,过度拟合是这种网络中的严重问题。大型网络也是使用缓慢,通过结合许多预测很难处理过度拟合测试时不同的大型神经网络。当训练数据比较少的时候,可能是数据采样噪声的原因导致在训练集上表现比较好,但是在测试集上表现不好,造成过拟合的现象.
基于上述问题,Dropout是用于防止过拟合和提供一种有效近似联结指数级不同神经网络结构的方法。如下图所示,dropout中的drop指随机“丢弃”网络层中的某些节点,一种简单的实现方式是每一个节点都有 p 概率被保留。对一个网络使用dropout相当于从网络中采样一个“变薄”的网络,这个变薄的网络包含所有节点(不管是存活还是被丢弃)。因此,一个有n个节点的网络可以看作拥有$2^n个“变薄”的网络的集合,这些网络共享权值,因此总的参数量还是O(n^2)或者更少。对于每一个训练样本,都有一个“薄网络”被采样训练,因此训练一个使用dropout的网络可以看成是在训练权值共享的$2^n个“薄网络”的集合。
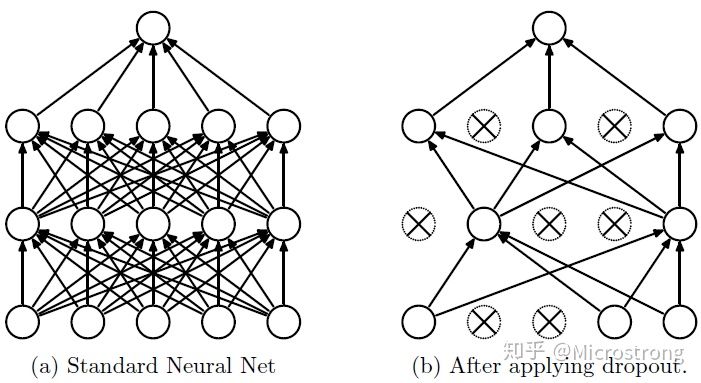
左边是正常神经网络隐藏层的神经元,右图是使用了Dropout的隐藏层神经元,虚线部分是随机隐藏了的神经元.
DropOut 工作流程
训练阶段
对于如下网络的训练流程一般是:把输入x通过网络前向传播然后把误差反向传播,网络进行学习后输出y。
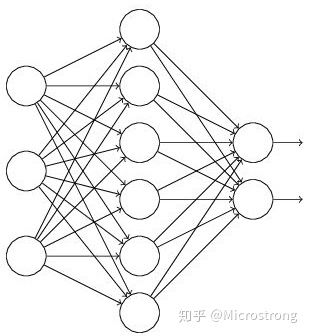
对于使用了dropout的网络如下:
- 以 1−p 的概率临时“丢弃”(p的概率保留)网络中的隐层神经单元.
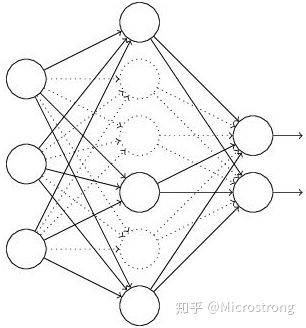
- 把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)。
- 恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
- 重复上述步骤1-3,知道网络结束.
测试阶段
显式地将训练中指数级的“薄网络”中求平均是不现实的。实践中的思路是这样:在测试时使用一个不使用dropout的网络,该网络的权值是训练时的网络权值的缩小版,即,如果一个隐层单元在训练过程中以概率p被保留,那么该单元的输出权重在测试时乘以p(如下图所示)。这样共享权值的$2^n$个训练网络就可以在测试时近似联结成一个网络,因此能有效降低泛化误差。
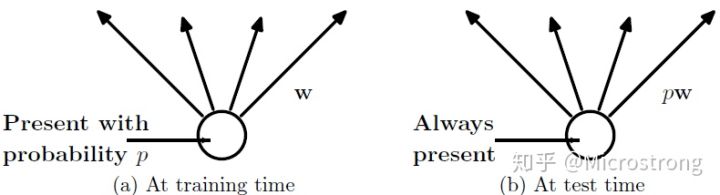
数学公式表示
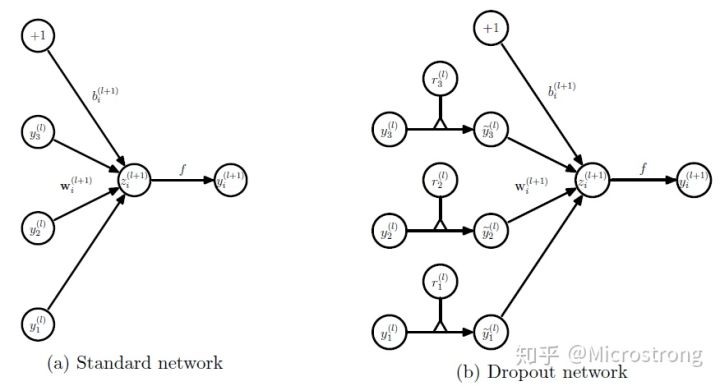
考虑一个拥有L层隐层的神经网络,l∈{1,…,L}为隐层的索引,z(l) 表示l层 的输入向量,y(l) 表示 l 层的输出(y(0)=x 为输入),W(l),b(l) 分别为 l 层的权值和偏置。标准的神经网络的前向传播可以描述为如下(对于l∈0,…,L−1 和任意隐层单元i):
z_i^{(l+1)} = w_i^{l+1} y^l + b_i^{(l+1)}
y_i^{(l+1)} = f(z_i^{(l+1)}) $$
其中$f$ 为任意激活函数,例如$f(x)=1/(1+exp(−x))$。
使用了dropout 之后前像传播过程如下:
$$ r_j^{(l)} \sim Bernoulli(p)
\hat{y}^{(l)} = r^{(l)} * y^{(l)}
z_i^{(l+1)} = w_i^{l+1} \hat{y}^{(l)}+ b_i^{(l+1)}
y_i^{(l+1)} = f(z_i^{(l+1)}) $$
其中∗代表element-wise相乘,对任意层$l,r(l)$从伯努利分布中采样,其值有$p$概率为1,采样后与该层的输出$y^{(l)}$进行element-wise乘积,产生一个“变薄”的网络层的输出$\hat{y}^{(l)}$,该输出随即用作下一层的输入。该过程应用在网络中的每一层。在test阶段,网络的权值按$W^{(l)}_{test}=pW_{(l)}$比例产生。
## Dropout可以解决过拟合原因
**降低神经元之间复杂的共适应关系**:神经网络(尤其是深度神经网络)在训练过程中,神经元之间会产生复杂的共适应关系,但是我们更希望的是神经元能够自己表达出数据中的共同本质特征。使用dropout后,两个神经元不一定每次都出现在同一个网络中,使得网络中的权值更新不再依赖于具有固定关系的神经元节点之间的共同作用,使得网络更加robust。
**模型平均**:Dropout使得神经网络的训练效果近乎于对$2^n$个子网络的平均,有可能使得一些“相反”的拟合互相抵消,从而缓解过拟合的情况。
## 参考文档
> 1. Dropout:A Simple Way to Prevent Neural Networks from Overfitting.